かけ算を「ハンコ」でイメージすると方程式も解ける！（二年生）

【難問にチャレンジ！】かけ算をイメージできれば、かんたんな方程式なら解ける！

※ここからは難しいので、子どもがわからないと言えば、いまは飛ばして構いません。あとでもう一度、勉強します。
※先にかけ算は「ハンコ」をイメージするとかんたん！から読んでください。ハンコがわからないと、このページに書いてあることは理解できないためです。

かけ算をハンコでイメージできると、かんたんな方程式も解けてしまいます。
論より証拠。
問題を見ていきましょう。

「〇×３」を計算すると９になりました。〇はいくつだと思いますか。

ふつうは「〇×３＝９」「〇＝９÷３＝３」と方程式で解くと思います。
しかし、現時点での子どもにはこれを理解するのは難しいので、「ハンコ」の話を使って説明するといいでしょう。小学校一年生でも簡単に理解できます。

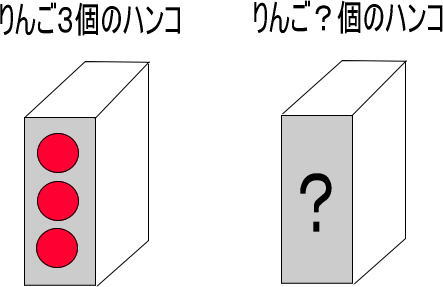
まずは、「〇×３」の「ハンコに、いくつ、りんごの絵があると思う？」と聞いてください。

「〇」がよくわからなくて、答えられないと思います。
「〇って、いくつかわからないってことなんだよ。とりあえず『？』にでもしておくよ。すると、こういうハンコになるよね」と言いつつ、紙につぎの絵を描いてください。

つぎに「ハンコは、何回、ポンッと押せばいいの？」と聞いてください。
「３回」と答えられればいいのですが、「〇」や「？」で頭がいっぱいで答えられない子どももいます。
そのときは、紙に「５×３」と書いて、「何回ハンコを押すんだっけ？」と、かんたんな数字を使って思い出させてください。
そうすれば「３回」と答えると思います。
その後、あらためて紙につぎのものを書いて、「ハンコは、何回、ポンッと押せばいいの？」と聞いてください。

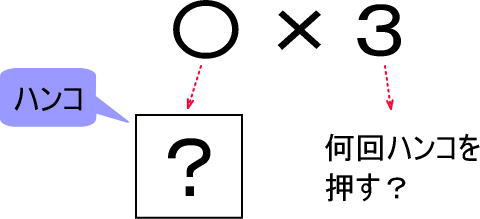
「３回」と答えられると思います。
そして、実際に、紙に「ハンコを押した絵」を描いてあげてください。
「？」の絵柄のハンコを３回押すわけなので、つぎのようになります。

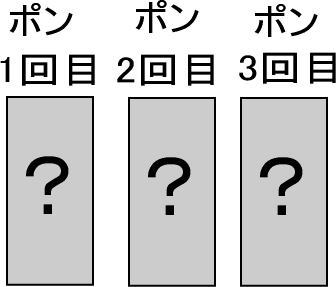
さて、ここでハンコの図を指して「ここにあるりんご、ぜんぶでいくつあると思う？」と聞いてください。
「９」と答える子どももいますが、ほとんどの子どもは、よくわからないという顔をすると思います。
そこで、「『４×３＝１２』は、ハンコに４個のりんごの絵があって、それを３回ポンと押すんだったよね。りんごの絵は全部でいくつになった？」と聞いてください。
「１２」と答えると思います。
そのとき、すかさず「『〇×３＝９』なわけだからりんごはぜんぶでいくつになる？」と聞いてください。
「９」と答えると思います。

ここからが肝心です。
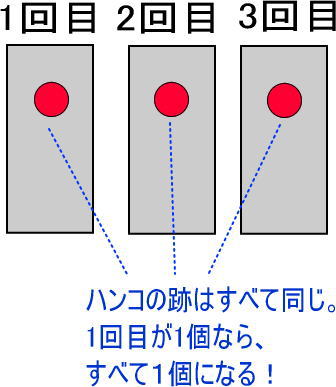
子どもに「ハンコなんだから、この３つ（ハンコの跡）まったく同じだよね？」と言ってください。
そして「もし、左端のハンコのりんごの絵が１つだったら、ほかのハンコの跡はどうなると思う？」と聞いてください。
ハンコの跡で、すべて同じなのだから、つぎのようになると気がつくと思います（気がつかなければ、そう教えてください）。
その後、「でも、これだと、りんごの数は全部で３つだよね。いま、全部で９個なのでちがうよね」と言ってください。

つぎは、左端のハンコの跡にりんご２個を描いてください。
「ハンコの跡だから、ほかのハンコの跡もリンゴ２つになるよね」と言いつつ、ほかのハンコの跡にもりんご２個を書きこんでください。
その後、「これも、りんごの数が６になるからダメだよね」と言ってください。

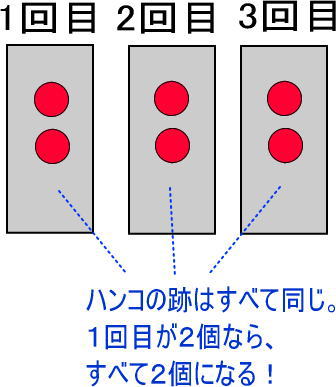
最後に、りんごが３個の図を描いてください。
「ハンコの跡だから、ほかのハンコの跡もリンゴ３つになるよね」と言いつつ、ほかのハンコの跡にもりんご３個を書きこんでください。
その後、「これだと、りんごの数は９個になるよね。これだよね！」といってください。

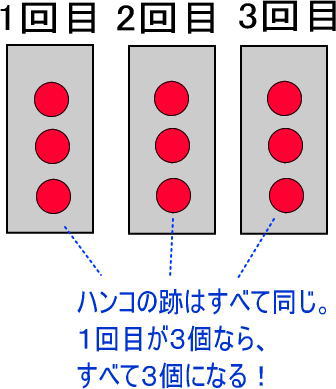
そして、「〇はいくつになる？」と聞いてください。
「３」と答えると思います。
答えられなければ「流れ」を復習するためにも、もう一度、説明してみてください。

もう一度、数字を変えて同じように説明してください。これで理解できなければ、時期尚早だったのかもしれません。もしくは、この考え方があわなかったのかもしれません。ここの話は飛ばしてください。
※この考え方があわなくても「面積図」という考えたかもあるのでご安心ください。面積図についても当サイトで解説しています。

【目標】「〇×３＝９」のような方程式が解ける。
【練習問題】つぎの方程式を解かせてください（ハンコの図を描かせて考えさせてください）。
あくまで、ここはかけ算のイメージを固めるのが目的です。係数が大きい方程式を解かせる必要はありません。

・〇×２＝４
・〇×２＝６
・〇×２＝８
・〇×２＝１０

・〇×３＝６
・〇×３＝９
・〇×３＝１２

・〇×４＝８
・〇×４＝１２

・〇×５＝１０
・〇×５＝１５

スポンサードリンク

【さらに難問！】「〇×２＋〇×３＝１５」の方程式を解かせてみよう！

方程式ができるようなら、さらに難しい方程式を解かせてみましょう。
紙に「〇×２＋〇×３＝１５」と書いて、「ハンコの図を描いてみて」と言ってください。

たいていの子どもはうまく図を描けないと思います。
何がわからないのかというと「＋」です。
そこで、「じゃあ、『３×２』のハンコの絵を描いてみて」と紙に絵を描かせてください。
子どもが絵を描くと「つぎは、『３×３』のハンコの絵を描いてみて」と絵を描かせてください。
なお、この際、最初の絵からすこし間をあけたところに、絵を描かせてください。
※「３×２」は「りんごの絵が３つあるハンコを２回押した」、「３×３」は「りんごの絵が３つあるハンコを３回押した」わけなので、つぎの絵になります。

子どもが絵を描けば「『３×』だから、両方とも同じハンコだよね。りんごの絵が３つのハンコ」と念押ししてください。

そして、つぎが肝心です。
「ハンコの跡はいくつある？」と聞いてください。

「５」と答えるのではないでしょうか。
※答えられないのならば「『３×２』でハンコを２回押したんだよね。つぎに『３×３』でハンコを３回押したんだよね。だから、合わせて５回じゃない？」と言うといいでしょう。

「３×２と３×３のハンコを合わせたら、ハンコの跡は５個になったってことだよね。『合わせる』わけだから、ここに『＋』を描いてもいいよね」と言いつつ、「３×２」と「３×３」の間に「＋」を描いてください。

子どもの顔を見てわかっていなさそうなら、別の例で説明してあげてください。

・「２×３」と「２×２」のそれぞれのハンコの絵を描かせます。
・「ハンコの跡は同じだよね？」「ハンコの跡がいくつある？」と聞く。
・「５」と答えれば、「『２×３＋２×２』としてもいいよね」と言う

ここがわかれば、あとはかんたんに理解させることができます。

問題に戻ります。
「〇×２＋〇×３＝１５」を解くのでした。

まずは「〇×２を、ハンコの絵で描いて」と言ってください。
すでに話していますが、子どもによっては忘れてしまっていることもあります。
繰り返して説明してあげてください。

間をあけて、その隣に「〇×３を、ハンコの絵で描いて」と言ってください。
子どもはすでに「〇×２」を描いているので、かんたんに描くと思います。

これら２つを合わせるわけなので、つぎの図になります。

同じ絵柄（「？」のこと）なので、すべて同じハンコです。
同じハンコを５回押したのと同じなので「〇×５」にできると教えてください。
ここまでくれば、もう子どもも理解できると思います。

よって「〇×５＝１５」となります。

あとは先ほど学習したのと同じです。
すべて同じハンコなので、もしハンコのりんごが１個だったとしたら、から考えます。

＜りんご１つの場合＞
同じハンコなので、ハンコのりんごが１つだとしたら、りんごは全部で５個になります。全部で１５個なので、りんご１つではありません。

＜りんご２つの場合＞
同じハンコなので、ハンコのりんごが２つだとしたら、りんごは全部で１０個になります。全部で１５個なので、りんご２つではありません。

＜りんご３つの場合＞
同じハンコなので、ハンコのりんごが３つだとしたら、りんごは全部で１５個になります。これが答えですね。

よって、〇は３になります。

スポンサードリンク

中学一年生の内容も理解させられるけど…。

りんごの絵が３つのハンコと、りんごの絵が５つのハンコは別のハンコですよね。
同様に、りんごの絵が〇のハンコと、りんごの絵が△のハンコは別のハンコだと理解させることができれば、中学一年生の内容も教えることができます。

しかし、このページをご覧になっているかたは、「子どもが、かけ算を習いはじめたころ」ですよね。
学年でいうと、幼稚園の年中から小学校低学年だと思います。

この時点で、中学一年生の内容を勉強させるのは意味がないとわたしは思いますので、この辺でやめておいたほうがいいと思います。